Here I take for granted that you are familiar with the general concepts introduced in the previous chapter regarding the interactions between atoms and molecules.
1The basic structure of DNA and RNA¶
Deoxyribonucleic acid (DNA) and ribonucleic acid (RNA) are the fundamental molecules that carry and execute the genetic instructions essential for all forms of life. Like proteins, they are macromolecules. However, the repeating monomer is not an amino acid, but a nucleotide, which is a molecule consisting of a a cyclic sugar (a pentose), a phosphate group, and a nitrogenous base. A nucleotide without the phosphate group is called a nucleoside.
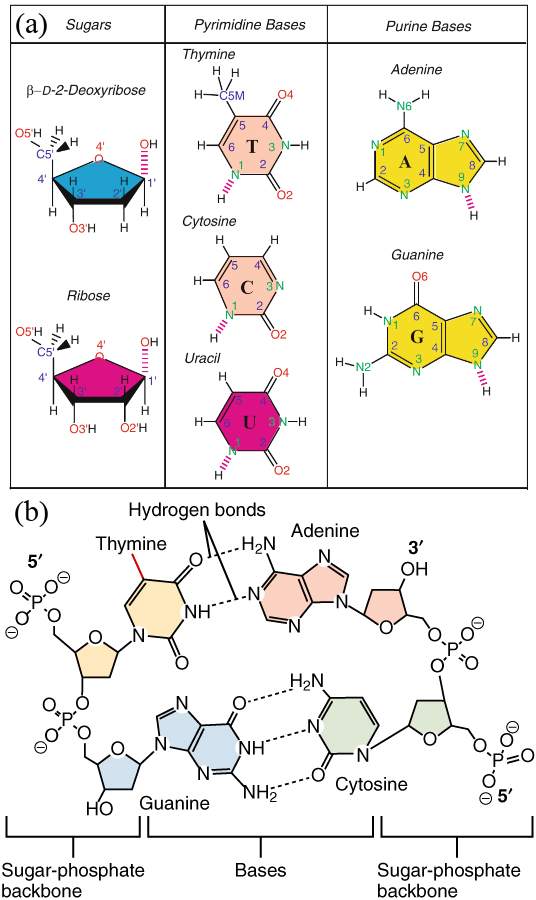
Figure 1:(a) The sugar and nitrogenous bases that make up DNA and RNA. Non-hydrogen atoms are labelled, and the broken lines indicate links that bind the compound to the other building blocks. Adapted from Schlick (2010). (b) A sketch showing two bonded DNA dinucleotides. The presence of a group connected to the pyrimidine ring highlighted in red makes the yellow-shaded base a thymine instead of a uracil. Adapted from here.
In the classic DNA double helix (or duplex) described by Watson and Crick, a flexible ladder-like structure is formed by two chains (strands) that wrap around a virtual central axis. The two chains’ backbones consist of alternating sugar and phosphate units, while the rungs that connect them consist of nitrogenous bases held together by hydrogen bonds and stabilised by stacking interactions. A schematic of a single nucleotide and of the Watson-Crick mechanism are shown in Figure 1.
Let’s briefly discuss the main building blocks of a nucleotide.
1.1The pentose¶
A pentose is a simple sugar (i.e. a monosaccharide) containing five carbon atoms. In nucleic acids, pentose is present in its cyclic form, where the ring contains four carbons and one oxygen. In DNA, one of the hydroxyl () groups is replaced by a hydrogen atom. This is not a small change since, as we already know, a hydroxyl group can be involved in a hydrogen bond.
The three-dimensional conformation of the five-carbon sugar ring in nucleotides is non-planar, and the ring can adopt various forms, with the C2’-endo and C3’-endo puckers being the most common forms for B-DNA and A-RNA (and A-DNA as well), which are helical structures that will be introduced in a moment. These puckering conformations, where the C2’ or C3’ atoms, respectively, are above the plane formed by the other four atoms, affect the overall structure and flexibility of DNA and RNA molecules and are one of the main source of conformational flexibility in nucleic acids (Schlick (2010)).
1.2The phosphate group¶
A phosphate group is, by definition, the same for DNA and RNA and is composed by a phosphate atom attached to four oxygens. When in its anion form, a phosphate can be written as : three of the oxygens are charged, and the fourth one is connected to the phosphate through a double bond. In nucleic acids, the phosphate group form a phosphodiester bond with the 3’ and 5’ carbon atoms of the pentoses of consecutive nucleosides, joining them together to form the strand’s backbone. I note here that you should not imagine the backbone as a rigid, fixed object, but as composed by segments around which the molecule can, to some extent, rotate. Indeed, there are six dihedral angles in the backbone (named, rather unoriginally, and ) that take different values depending on the local conformation (see Schlick (2010) for more details).
Finally, as shown in Figure 1(b), a phosphate that connects two nucleotides has a single residual negative charge. By contrast, phosphates at the beginning of a strand (also known as the 5’ end) are doubly charged.
1.3The nitrogenous base¶
The nitrogenous bases endow the monomer with the exquisite selectivity that underlie the Watson and Crick double helix. Nitrogenous bases found in nucleic acids are
Purines, molecules with five- and a six-membered rings fused together: guanine (G) and adenine (A), present in both DNA and RNA.
Pyrimidines, molecules with a single six-membered rings: cytosine (C), present in both DNA and RNA, thymine (T, DNA-only), uracil (U, RNA-only)[1].
The chemical structure of the bases are shown in Figure 1(b). Note that uracil has the same chemical structure as thymine, minus the group connected highlighted in red in the figure. Each base is connected to the C1’ atom of the corresponding pentose through a nitrogen, which results in a glycosyl bond around which the base can rotate, contributing to the flexibility of the polymer. The dihedral angle associated to this rotation is called .
In the classic pairing scheme unveiled by Watson and Crick, the geometry of the bases is such that G binds only to C, and A binds only to T (or U in RNA) by means of three and two hydrogen bonds, respectively. Additional non-canonical base pairings that are not only possible, but also biologically relevant exist. Here I will mention wobble base pairs, where G can bind with U[2] with a thermodynamic stability that is similar to that of canonical base pairs, and Hoogsteen base pairs, where nucleotides can bind with an alternative geometry that can drive the formation of uncommon secondary structures such as triple-stranded helices or G-quadruplexes.
1.4Chain polarity¶
As mentioned earlier, the phosphodiester bond links the C5’ atom of a nucleotide with the C3’ atom of the one the follows it. As a result, DNA and RNA strands have a polarity, i.e. they are inherently directional. By convention, a strand starts at the group (termed 5’ end or terminal) and ends at the group (the 3’ end or terminal), and its sequence is also specified in this way. This is important since, as we will discuss in a moment, only anti-parallel strands (or anti-parallel sections of the same strand) can pair and form secondary structures.
1.5Hydrophobicity and hydrophilicity¶
The nitrogenous bases have both hydrophobic and hydrophilic regions: the aromatic ring structures have hydrophobic properties, but they also contain functional groups that can form hydrogen bonds, contributing to some degree of hydrophilicity. However, the partial hydrophobic character of the bases is more than counterbalanced by the backbone, which is highly hydrophilic due to the negatively charged phosphate groups and to the hydroxyl groups () of the sugar that can form hydrogen bonds with water. As a result, nucleotides readily dissolve in water.
The strong hydrophilic character of DNA and RNA strands makes their tertiary structure somewhat simpler compared to proteins, since once the secondary structure elements are formed, there is no strong interaction driving the formation of tightly packed super-secondary or tertiary structures[3].
1.6Hybridisation and denaturation¶
Two nucleotides coming together and binding to each other form a base pair (BP). Since hydrogen bonds are highly directional, HB formation requires that the two nucleotides approach each other with the right mutual orientation. However, note that bases on their own (i.e. not part of a strand) can pair with any other base, as well as with themselves, often with more than one arrangement (Voet & Rich (1970)). It is only in an extended paired region that the correct orientation is obtained only if the two nucleotides are compatible (i.e. if they can form a canonical or a non-canonical base pair, as mentioned above), and the strands run anti-parallel to each other. In this geometry, which is adopted by the most common DNA and RNA helical conformations,
the bases on one strand can align perfectly with their complementary bases on the opposite strand, allowing stable hydrogen bonding;
the sugar-phosphate backbones run in opposite directions, allowing the bases to stack neatly on top of each other, contributing to the overall stability of the double helix through van der Waals forces and hydrophobic interactions;
negatively charged phosphate groups on the sugar-phosphate backbone are positioned in a way that minimizes repulsion.
Interestingly the spontaneous process through which single strands pair and form a duplex, which is called hybridisation, is now taken for granted, but was initially met with skepticism[4], since researchers at the time believed that duplex formation required enzymes to overcome electrostatic and entropic penalties (Rich (2009)).
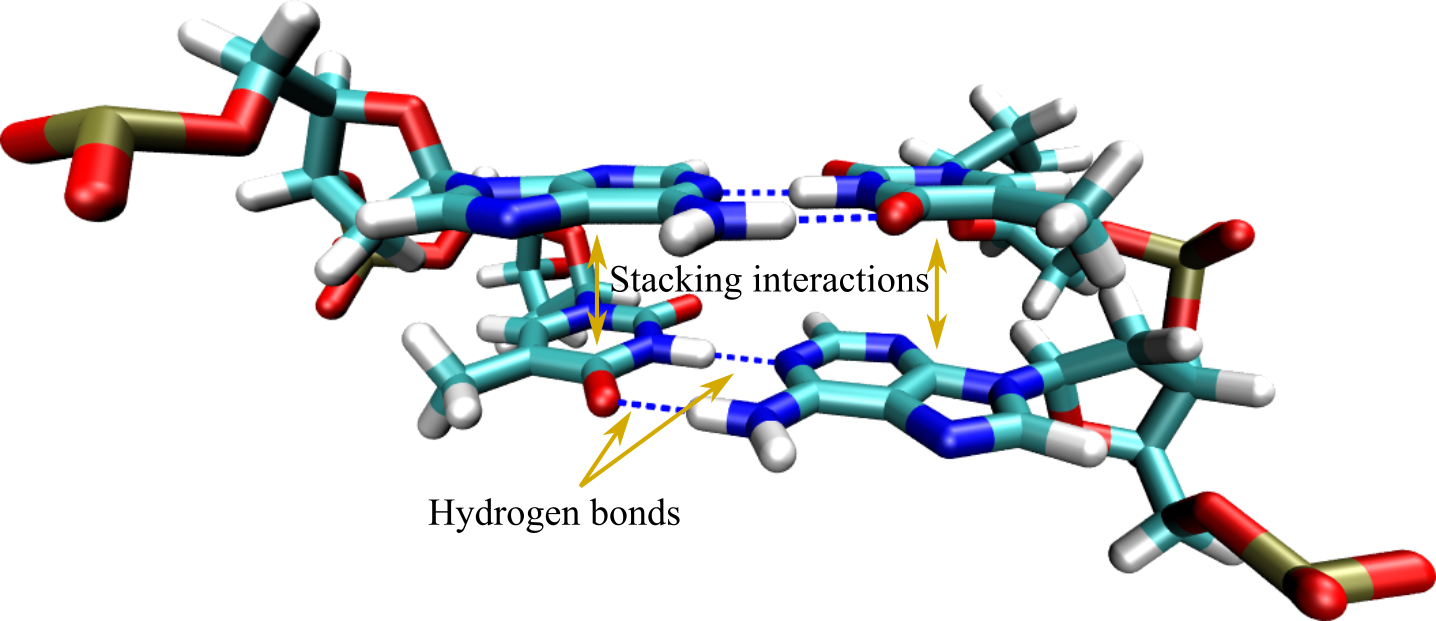
Figure 3:A base pair step where hydrogen bonds and stacking interactions, the two main mechanisms responsible for hybridisation, are highlighted by arrows.
In addition to hydrogen bonding, duplexes are stabilised by interactions acting between the aromatic rings of consecutive nitrogenous bases (see Figure 3). These so-called base stacking interactions have a hydrophobic nature that is complemented by van der Waals and dipole-dipole terms that contribute significantly to the stability and structural integrity of the DNA molecule. Rather counterintuitively, there is now ample evidence that base stacking is at least as important for duplex stability as base pairing, if not more (see e.g. Yakovchuk (2006), Vologodskii & Frank-Kamenetskii (2018), and Banerjee et al. (2023)).
The hybridisation of complementary strands is an enthalpy-driven process, and therefore it is promoted by a temperature decrease: at high temperature, where entropy dominates, the two strands are separated. As decreases, the energetic gain of forming BPs progressively leads to the stabilisation of the duplex. Strand hybridisation is a cooperative transition characterised by melting temperature and width that are controlled by the sequence, as well as by the buffer conditions (pH, ionic strength, etc.).
The transition is fully reversible: a duplex can be separated into its two composing strands (i.e. melted or denatured) by raising the temperature sufficiently.
2Secondary structure¶
Hydrogen bonding and base stacking drives are the main drivers for the formation of secondary structure in nucleic acids which, akin to the secondary structure of proteins, refers to the local conformation taken by polynucleotide chains. In the biological setting there is a marked difference between the possible secondary structures of DNA and RNA. Indeed, the secondary structure of biological DNA is rather boring, as it tends to form long and stable double-stranded helices storing the genetic code. By contrast, the secondary structure of biological RNA is more diverse, owing to the additional hydroxyl group present in the sugar, and to the fact that RNA is nearly always found as a single strand. Its complex secondary structure allows RNA to fulfill its many roles in processes such as catalysis, regulation, and protein synthesis.
Assuming that each base can either be unbound or involved in a single base pair[5], the secondary structure of nucleic acids is defined by the pairing information of the nucleotides. By assigning a unique index to each nucleotide, this information can be represented as a list of index pairs, where each entry represents a single base pair. While, as I mentioned already, there are key differences between DNA and RNA, the surge of DNA nanotechnology has blurred the boundaries between the two, and many of the secondary structures that were unique to RNA can also be found in synthetic DNA systems. As a result, in this part I will refer to generic “nucleic acids”, if not explicitly stated otherwise.
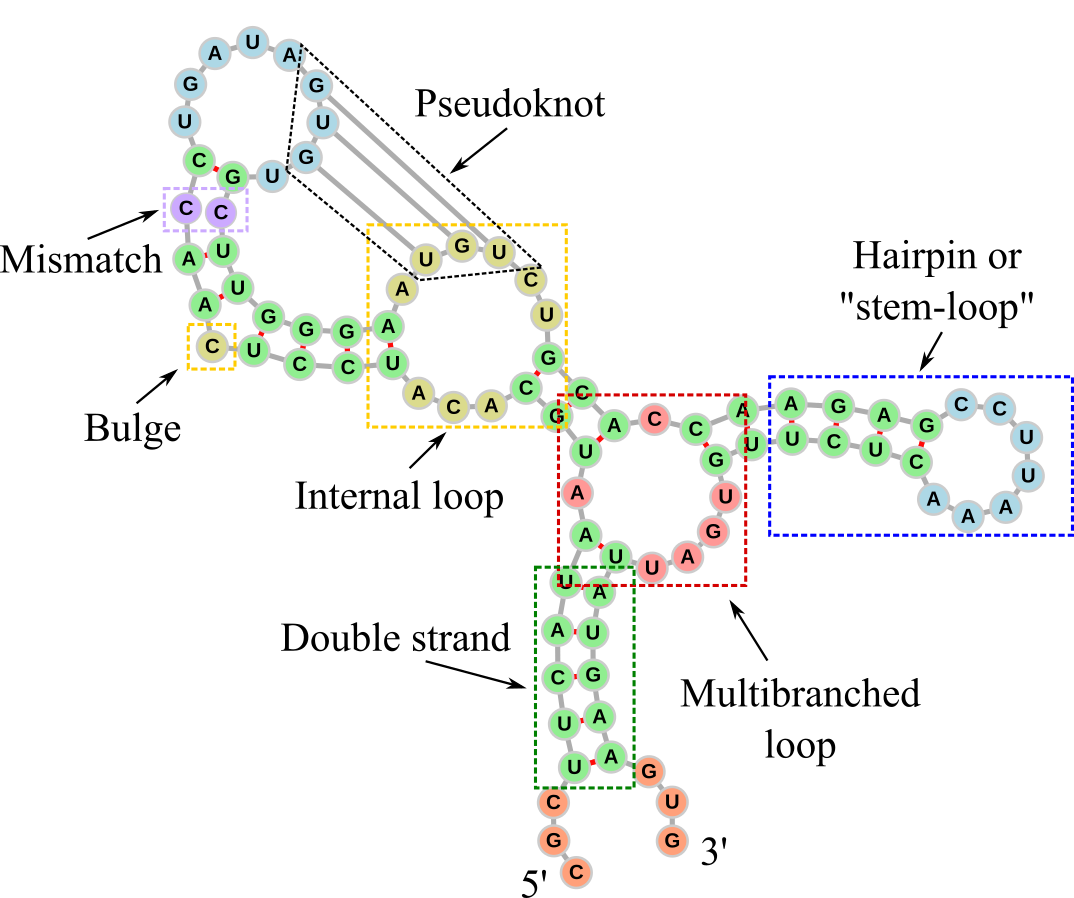
Figure 4:The secondary structure of an RNA molecule. Dashed rectangles and labels have been added to the different elements. The double-stranded parts are coloured in green, while the other colours are used to highlight the other main secondary structures: 5’ and 3’ unpaired regions in orange, internal loops and bulges in yellow, internal loops of size one (also known as mismatches) in violet, hairpin loops in blue, multibranched loops in red. The graph representation has been generated with forna.
Figure 4 shows the secondary structure of an RNA molecule drawn as a graph, which is a common representation. The backbone runs from the 5’ to the 3’ end and it is drawn with grey sticks representing the graph’s edges, while the single nucleotides are the vertices, drawn as circles. Base pairs are depicted with red connections. The RNA molecule has been designed to feature the main secondary structure motifs, which are highlighted by coloured dashed rectangles. These are:
Double-stranded part: Sections made of consecutive base pairs.
Hairpin (also known as a stem-loop structure): A single strand that folds back on itself to form a stem-loop structure. The stem is a double-stranded region where bases pair with complementary bases, and the loop is a single-stranded region at the tip.
Bulge: Occurs when one or more unpaired nucleotides bulge out from one side of a double-stranded stem.
Internal loop: Formed when there are unpaired nucleotides on both sides of the double-stranded stem, creating a loop in the middle of the stem. An internal loop made of one nucleotide on each strand is often called a mismatch.
Multibranched loop: A loop where three or more double-stranded stems converge.
Pseudoknot: Formed when bases in a loop pair with complementary bases that are separated by at least one double-stranded section. This results in a crossover of strands, forming a knot-like structure. A common way a pseudoknot forms is when a single-stranded loop of a hairpin pairs with a complementary sequence outside the hairpin.
2.1Dot-paren notation¶
Dot-paren notation provides a clear and concise way to represent the secondary structure of nucleic acids, showing which nucleotides are paired or unpaired, regardless of their identity. It is a useful tool for storing information about complex secondary structures, and for exchanging this information to and from computational tools.
The dot-paren notation uses dots and parentheses to indicate unpaired and paired nucleotides, respectively.
Unpaired Nucleotides:
Dots (.) represent nucleotides that are not involved in base pairing.
Example:
....represents four unpaired nucleotides.
Paired Nucleotides:
Parentheses indicate base pairs, with matching opening and closing parentheses representing the paired nucleotides.
An opening parenthesis
(signifies the 5’ end of a base pair, while a closing parenthesis)signifies the 3’ end.A well-formed dot-paren representation should have the same number of opening and closing parentheses.
Hairpins:
Hairpin loops are represented with a series of dots inside parentheses.
Example:
(((....)))indicates a stem of three base pairs with a loop of four unpaired nucleotides.
Bulges and Internal Loops:
Bulges are unpaired nucleotides on one side of a stem.
Internal loops have unpaired nucleotides on both sides.
Example:
((..((...))..))represents a structure where there is a small internal loop of size 2 within a larger stem, while((.(...)))represents a stem-loop with a single bulge.
Multibranch Loops and Pseudoknots:
Multibranch loops involve multiple stems and are, in general, complex to represent.
Pseudoknots, which involve base pairs crossing one another, are not well-represented by simple dot-paren notation but can be indicated with additional notation if necessary (see the complex example in the box below).
There are other formats to store nucleic acid secondary structures that overcome some of the problems with the dot-paren notation (pseudoknot representation, lack of multi-strand support, poor readability, etc.), but none has become a standard yet. You can look at some examples here or here.
2.2Nearest-neighbour models¶
Nearest-neighbour (NN) models for nucleic acids are computational frameworks used to predict the thermodynamic stability and secondary structure of DNA and RNA molecules. These models operate on the principle that the stability of a base pair is influenced primarily by its immediate neighbors rather than by more distant sequences. As we already know, base stacking and hydrogen bonding are the main drivers for the formation of helical structures. Therefore, assuming that the stability of nucleic acid structures is determined primarily by the local sequence context (the identity and orientation of adjacent base pairs), the complex interactions within nucleic acids can be simplified by considering only the contributions of dinucleotide pairs, hence the “nearest-neighbour” name.
The most used NN models are:
The SantaLucia model for DNA (SantaLucia & Hicks (2004))
The Turner model for RNA (Lu et al. (2006))
In addition, here is a useful website where several NN models are briefly described, and their parameters can be downloaded.
In general, a NN model is defined by a list of contributions that make it possible to assign a free-energy cost to the secondary structure of a specific strand (or system of strands) in an additive way: the total free-energy cost of the structure is given by a sum of terms that refer to the sequence and type of each local secondary structure. The specific values that enter into the calculations are being constantly improved upon by means of careful experiments on many different sequences (similar in spirit to those performed to obtain the sequence-dependent stacking strength, see the box above). A recent example is Zuber et al. (2022). By contrast, the functional forms and the nature of the different free-energy terms are rather stable and did not change much in the last 20+ years.
The contributions are given in terms of and or and , which are linked by the relation
where the ° superscript signals that these values refer to the free-energy differences estimated at the “standard” strand concentration of 1 molar (i.e. one mole per liter), .
We now analyse the main free-energy contributions to the formation of secondary structures used in NN models.
2.2.1Nearest-Neighbor Interactions¶
Double-strand formation is driven by the combined effects of base stacking and hydrogen bonding between adjacent base pairs. In NN models, these are accounted for by summing up the enthalpy and entropy contributions of each dinucleotide base step. Therefore, for a sequence of length there are terms. As an example, consider the two fully-complementary strands
5'- TACCTG -3'
3'- ATGGAC -5'In order to estimate the free-energy, we split the sequence into dinucleotide steps:
5'- TA AC CC CT TG -3'
3'- AT TG GG GA AC -5'so that the total contributions due to this term are given by
2.2.2Terminal penalty¶
Most NN models requires adding a correction term to the free energy that depends on the base pair at each end of the helix. In most cases the penalty is present only if the terminal base pair is AT (or TA) and it tends to be rather small. Therefore, it is important only for short sequences.
2.2.3Initiation and Symmetry Terms¶
The formation of a double helix requires an initial free-energy input to overcome entropy and start the pairing process. The term has to be added once per contiguous double-stranded region or helix.
In the presence of self-complementary duplexes (i.e. if the sequence of the two strands composing a duplex is palindromic), there is an additional purely entropic term that takes into account the fact that a strand can pair with a copy of itself. Here is an example:
5'- AGCGCT -3'
3'- TCGCGA -5'2.2.4Loop Free Energies¶
Forming hairpins, bulges, external, internal or multibranched loops costs both entropy (since we constrain the strand backbone) and enthalpy (since the backbone has to be bent or twisted to some extent). These free-energy penalties are, in general, sequence-dependent, but the number of possible combinations grows exponentially with the loop size. Therefore, the free-energy cost of these motifs is usually approximated to depend only on the loop size (with some exceptions such as hairpins with loops of length three and four, see e.g. SantaLucia & Hicks (2004)).
2.2.5Penalties for Mismatches and Terminal Mismatches¶
Non-complementary paired bases have a destabilising effect on secondary structure. The specific energetic penalty that applies depend on the sequence of the mismatch, but also whether it occurs at the ends of helices (terminal mismatches), or within the helix (internal mismatches, sometimes referred to as “1x1 internal loops”. Both reduce the overall stability of the structure compared to fully-complementary sequences, but to different extents. The following example contains both types of mismatches (look at the first and fifth base pairs):
5'- CTACACTG -3'
3'- TATGCGAC -5'2.2.6Dangling Ends¶
Dangling ends refer to unpaired nucleotides at the 5’ or 3’ ends of a helix that can stabilise specific secondary structures such as multibranched and exterior loops through additional stacking interactions. For instance, in this example the top strand has both a 5’ and a 3’ dangling end:
5'- ATACCTGC -3'
3'- ATGGAC -5'These terms tend to be sequence-dependent: in the example above, the contribution of the 5’ dangling end would be different if the sequence was TT/A or AC/A instead of AT/A. Note that a helix end extended on both strands has a terminal mismatch rather than two dangling ends.
2.2.7Coaxial Stacking Parameters¶
Coaxial stacking refers to the stacking interactions between adjacent helices in branched or complex secondary structures, such as those found in multibranched loops or multi-strand systems. These interactions can significantly stabilize the overall structure by allowing helices to stack on top of each other in a manner similar to base stacking within a single helix.
In most NN models, two types of coaxial stacking are handled: when two helices are directly adjacent and no intervening unpaired nucleotides are present (“flush coaxial stacking”), or when a single mistmatch occurs between the stacked helices (“mismatch-mediated coaxial stacking”). The following examples (taken from here) show the two cases, where the backbone is explicitly drawn using dashes:
5'- C-A-G-A -3'
3'- G-U C-U -5'
| |
G A
| |
5'3'5'- C-A-G-A -3'
3'- G-U A-U -5'
| |
G A
| |
5'3'2.2.8Salt-Dependent Terms¶
The stability of nucleic acid structures is influenced by the ionic environment, since cations like Na and Mg shield the negative charges on the phosphate backbone and reduce electrostatic repulsion between strands. Note that, as far as I know, only the SantaLucia NN model for DNA, presented in SantaLucia & Hicks (2004), takes into account this contribution through the following entropic term:
where is the number of phosphates in the duplex, so that is, under usual conditions, the duplex length, is the molar concentration of monovalent cations[8], and the resulting contribution is in units of cal / mol K.
2.3The two-state model¶
2.3.1Duplex formation¶
One of the most straightforward applications of any NN model is to model the thermodynamics of duplex formation in a system composed of just two (perfectly or partially) complementary strands, A and B. If the sequences are such that the possibility of stable intermediates can be neglected (that is, if the strands spend most of the time either free in solution or bound to each other), hybridisation can be described as a two-state process[9]. The latter, in turn, is formally equivalent to the chemical equilibrium between two reactants and a product, viz.
The two-state model works particularly well for short strands (i.e. oligonucleotides) since, if they do not contain repeating patterns or similar “pathological” sequences, they are more unlikely to exhibit metastable intermediates, i.e., states with secondary structures whose stability can almost match that of the product.
Under the two-state assumption, equilibrium is described by the law of mass action equation
where is the (molar) concentration of and is the dissociation constant associated to the reaction. This relation can be derived directly from the condition of thermodynamic equilibrium. In an ideal dilute solution, the chemical potentials of the three species satisfy
where is the chemical potential of species in an ideal dilute solution, and denotes its standard-state chemical potential, defined as the molar Gibbs free energy of at M concentration. Combining the two expressions above gives
Since in units of kcal/mol the difference between the chemical potentials is the free-energy difference between the two states (with the minus sign, given the convention of NN models), , we write
and therefore
Hence, the law of mass action emerges as a direct consequence of the equilibrium condition under ideal-solution assumptions, where intermolecular interactions other than duplex formation are negligible and the species are well mixed.
Alternatively, one may view this result from a kinetic standpoint: in a dilute system, the rate of association is proportional to the probability that an and molecule encounter each other, , while dissociation occurs at a rate . At equilibrium, detailed balance implies , leading once again to the same mass-action form, with .
We define the concentrations of the two isolated strands (i.e. when ) as and , so that the total strand concentration is . Without loss of generality we assume that .
Every time a duplex forms, the number of A and B strands decreases by one each, so that the total strand concentration can be written as . We first compute the melting temperature , which is the temperature at which half of the duplexes are formed. Under this condition, , since the number of duplexes that can form is controlled by the number of strands in the minority species, so that Eq. (12) becomes
which, recalling that , can be used to obtain the following expression for :
However, since , and, by definition of melting temperature, , so that , we find
In the common case of equimolarity, i.e. when , Eq. (15) simplifies to
The denominator of Eq. (16) can be rewritten as , where
is a renormalised entropy difference that takes into account the concentration at which the reaction takes place. Using Eq. (17) makes it possible to directly derive the free-energy difference between the and states at any strand concentration. In the general case , the additional entropic factor is .
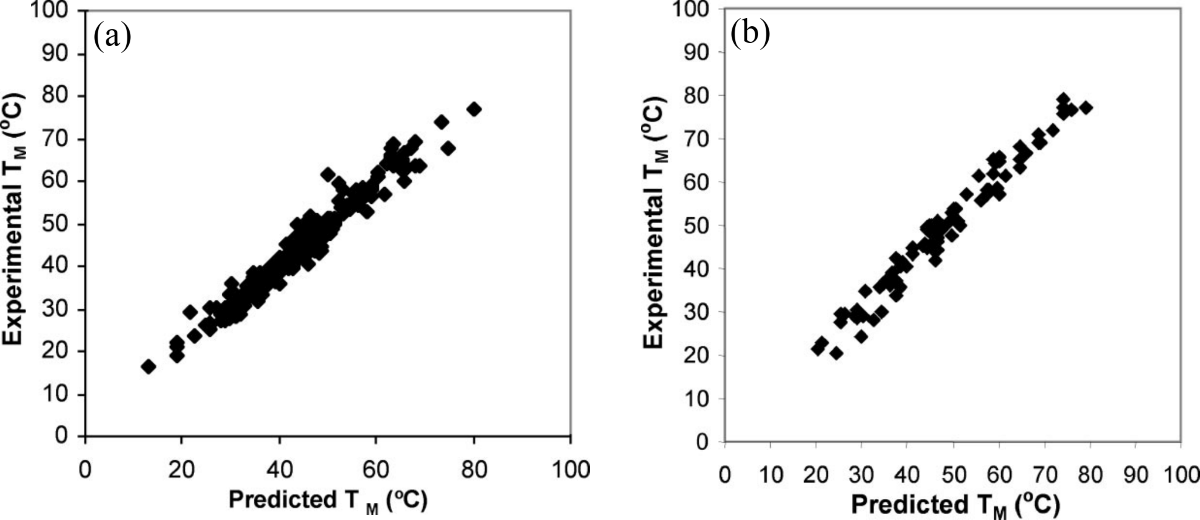
Figure 6:Experimental versus predicted melting temperatures of DNA oligonucleotides. (a) Data for 264 duplexes of length 4 to 16 bp in solution with 1 M of NaCl. (b) Data for 81 duplexes of length 6 to 24 bp in solution with variable NaCl concentration ranging from 0.01 to 0.5 M. Adapted from SantaLucia & Hicks (2004).
Figure 6 shows a comparison between the experimental and theoretical melting temperatures of hundreds of DNA oligonucleotides predicted with the SantaLucia model. The average absolute deviation is smaller than 2.3 K.
2.3.2Hairpin formation¶
Hairpin formation can also be modelled as a two-state process, where the equilibrium is between the open (random coil) and closed (stem-loop or hairpin) states:
In this case the overall strand concentration does not play any role[10], and the dissociation equilibrium is given by
where and are the concentrations of strands in the coil and hairpin conformations, respectively, and is the free-energy difference between the two states. The condition for the melting temperature is , which yields
2.3.3Melting curves¶
We now consider a generic nucleic acid system where one or more strands can pair and/or fold into a product P. We define the melting curve as the yield of P, in terms of concentration or fraction of formed product, as a function of temperature or another thermodynamic parameter that is changed experimentally, such as pH or salt concentration.
I will now show how the same two-state formalism introduced ealier can be used to predict the melting curve of a system. For the sake of simplicity I will use the system with . Defining as the probability that a strand is not part of a duplex, the equilibrium concentrations can be written as and . Substituting these relations in Eq. (12) and simplifying common factors we find
where we have used the renormalised entropy to obtain the latter relation. Resolving for and taking the positive root we find
From the duplex yield can be computed as (which is the probability that a strand is in a duplex), and the duplex concentration as .
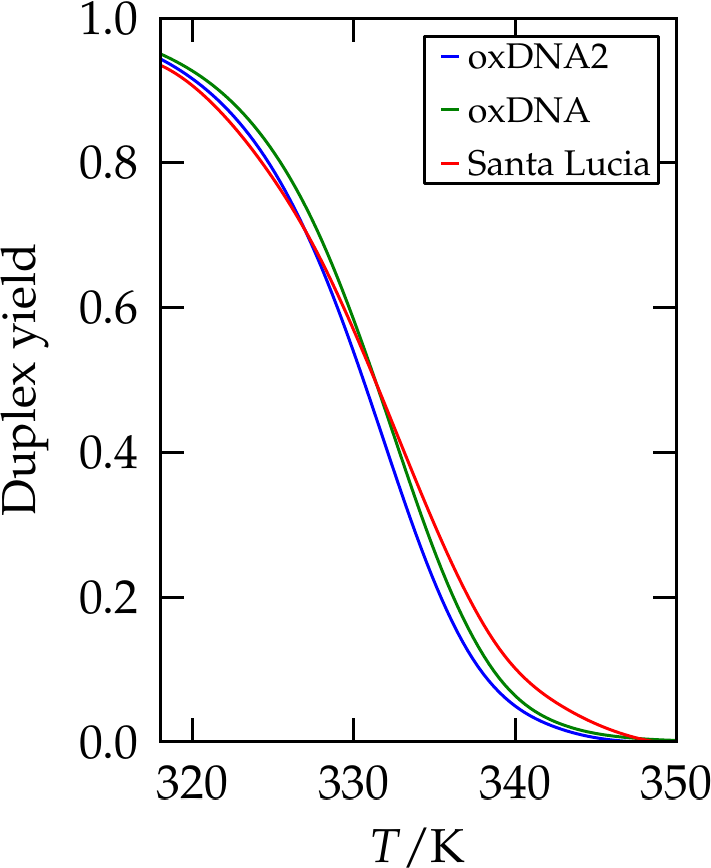
Figure 7:The yield of a 10-bp duplex as predicted by SantaLucia (red line), and two coarse-grained simulation models, oxDNA and oxDNA2. Adapted from Snodin et al. (2015).
Figure 7 shows the yield of a oligonucleotide of 10 bp as predicted by the SantaLucia NN model and by simulations of two coarse-grained models.
3Tertiary structure¶
The tertiary structure of nucleic acids is, in general, much simpler than that of proteins. This is due to the more limited variety of building blocks involved (4 vs 20), and to the charged (and, in general, hydrophilic) nature of the DNA and RNA backbones, which tend to destabilise the type of “super-secondary structures” that are so common in proteins. Moreover, the lack of tightly-packed structures blurs the difference between secondary and tertiary structures, since most of the times, especially in simple systems, the tertiary structure is straightforwardly implied by the secondary structure.
In general, the most dominant tertiary structure of RNA and DNA is the double helix, and is the main one we will consider going forward. Many different helical structures have been discovered in biological contexts or synthesised artificially under specific conditions. However, here I will present only the three main (“canonical”) ones. Note that I will provide only an average characterisation for each helix, as it is known that their properties can depend (even strongly in some cases) on the local sequence. You can use this webserver (which is presented in Sharma et al. (2023)) to visualise the 3D structures of a given sequence, as estimated with a coarse-grained, realistic model.
3.1Canonical helices¶
When two complementary strands pair together, they wrap around each other and form a periodic helical structure. The type of the resulting helix depends, in general, on the strand type (DNA or RNA), external conditions (ionic strength, pH, water concentration, etc.), and sequence.
3.1.1B-DNA¶
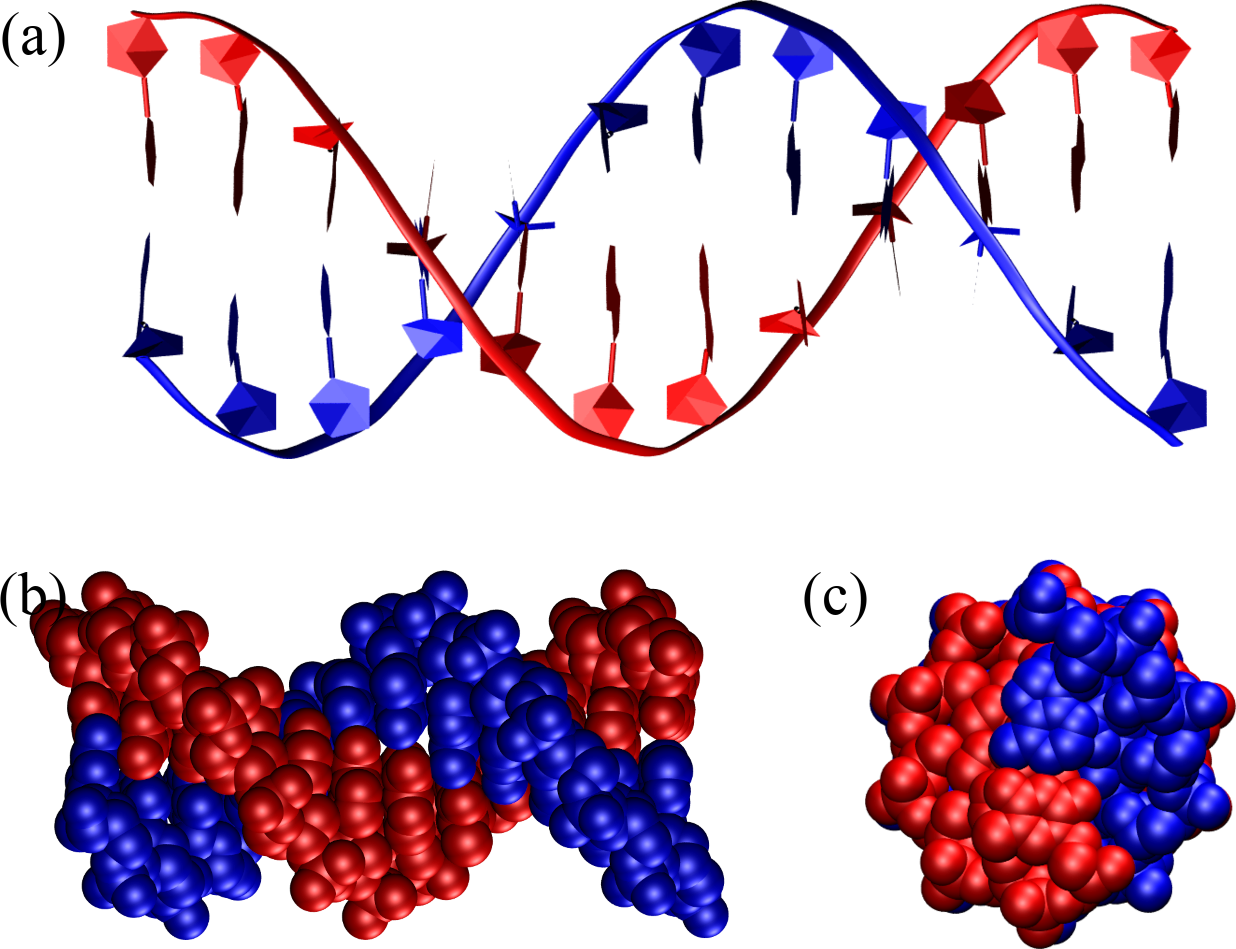
Figure 8:A B-DNA double helix composed of 12 base pairs as seen from the side, (a) and (b), and from the top (c). In (a) the backbone is represented as a ribbon, the sugar as a pentagon and the bases are outlined as pentagons and hexagons, while (b) and (c) shows the atoms as van der Waals spheres. The structure has been generated with the 3DNA 2.0 webserver.
The single most important conformation of DNA is B-DNA, which is the famous double helix whose structure was described for the first time by Watson and Crick. B-DNA is a right-handed helical structure that consists of about 10.5 base pairs per turn, with a diameter of approximately 2 nanometers. The structure features major and minor grooves, which are essential for protein-DNA interactions; the major groove is wide and deep, while the minor groove is narrow and shallow. B-DNA is most stable under physiological conditions, making it the prevalent form in biological systems. As described in the box above, the famous experimental photo that was instrumental for Watson and Crick’s discovery was taken by a student of Rosalind Franklin, who gave its name not only to B-DNA, but also to A-DNA, which is another canonical form of DNA.
Figure 8 shows a perfect B-DNA helix with different representations and from two different points of view. In panel (a) the representation makes it easy to see that
The strands run in an anti-parallel fashion: look at the orientation of facing pentagons, or at the way bases are connected to the sugars.
Base pairs have essentially zero inclination with respect to the helical axis.
3.1.2A-DNA and A-RNA¶
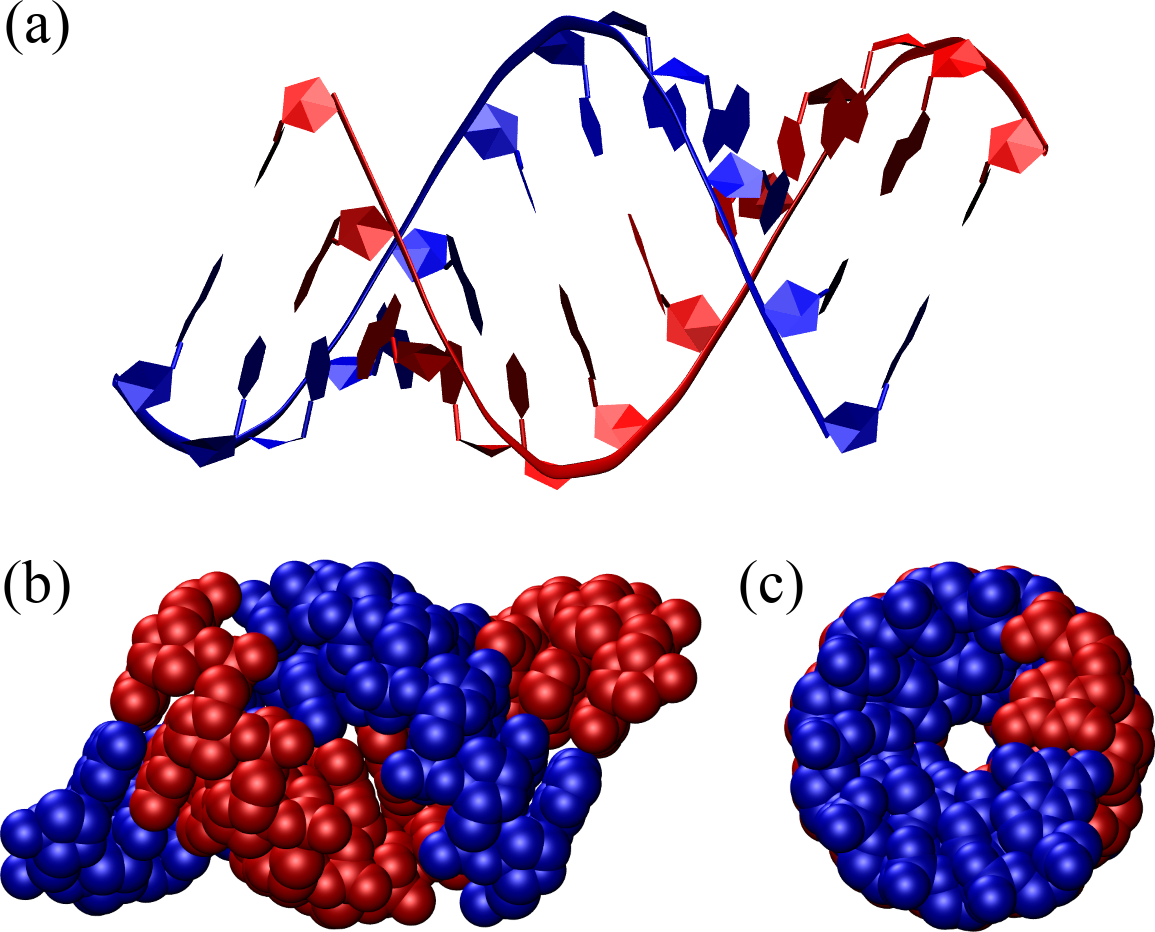
Figure 9:An A-DNA double helix composed of 12 base pairs represented as in Figure 8. The structure has been generated with the 3DNA 2.0 webserver.
DNA turns into its A form when dyhdrated, which can happen as a result of human intervention (e.g. when crystallising samples to study with X-rays), but also under natural conditions, when water is scarce or specific proteins bind to the DNA, in place of some of the water molecules[11]. A-DNA is a right-handed helix that is more compact than B-DNA: it has about 11 base pairs per turn and a diameter of approximately 2.3 nanometers. A-DNA features deeper major grooves and shallower minor grooves compared to B-DNA. The helical structure is more tightly wound, with the base pairs tilted by abouy relative to the helix axis, and the distance between base pairs is shorter. Moreover, the sugars are in the C3’-endo conformation rather than in the C2’-endo conformation like in B-DNA. A-DNA is less prevalent in biological systems but can be found in certain DNA-RNA hybrids. Additionally, double-stranded RNA molecules or regions typically adopt the A-form helical structure.
Figure 9 shows a perfect A-DNA helix made of the same number of base pairs as the one shown in Figure 8. Compared to B-DNA, it is evident that A-DNA is shorter and thicker, and the base pairs are inclined by with respect to the helical axis.
3.1.3Z-DNA¶
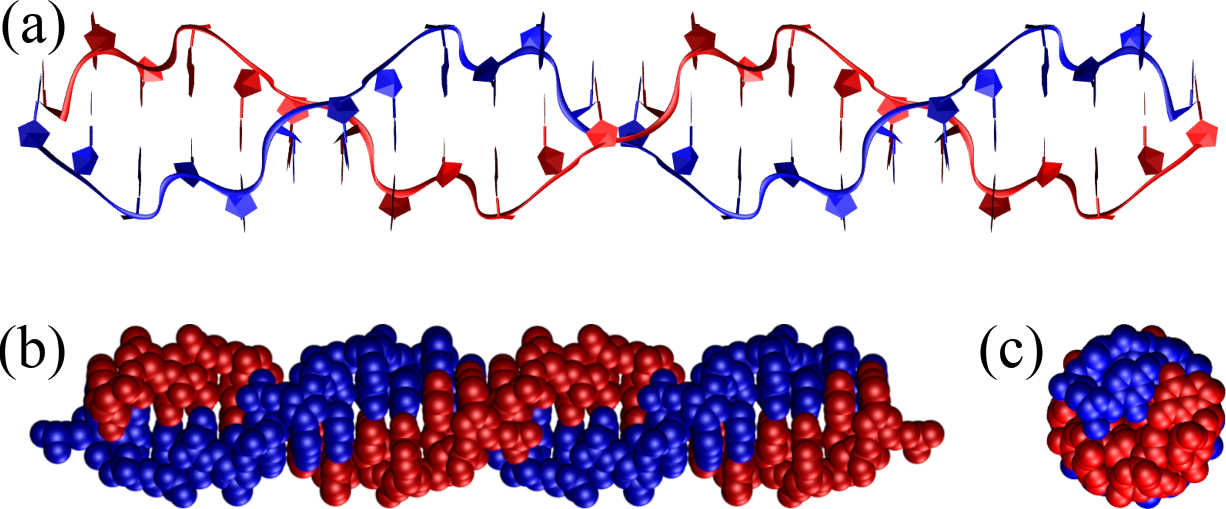
Figure 10:A Z-DNA double helix composed of 12 GC base steps (i.e. 24 base pairs) represented as in Figure 8. Note the zig-zag pattern drawn by the backbone, which gives Z-DNA its name. The structure has been generated with the 3DNA 2.0 webserver.
Another important DNA conformation is Z-DNA, which is a less common and structurally distinct form of DNA characterized by a left-handed double helical structure, in contrast to the right-handed helices of A-DNA and B-DNA. It has a zigzag backbone, which gives Z-DNA its name, and consists of about 12 base pairs per turn with a diameter of approximately 1.8 nanometers. The major and minor grooves are less distinct in Z-DNA, and the structure is more elongated and thinner. Z-DNA requires a specific sequence of alternating purines and pyrimidines (e.g. repeating GC steps) and can form under high salt conditions or negative supercoiling, i.e. twisting of the DNA in the left-handed direction. Though less prevalent than B-DNA, Z-DNA is thought to have important biological functions in gene regulation, genetic recombination, and in the context of certain protein-DNA interactions.
Figure 10 shows a perfect Z-DNA helix made of 24 base pairs (12 repeating GC steps) which shows the main features of Z-DNA: the left handedness of the helix, the zig-zag pattern that gives this conformation its name, and the small BP inclination.
A comparison between the average properties of the three main helical conformations is shown in Table 1.
Table 1:The main (average) properties of the three canonical forms of DNA and RNA.
| Form | Handedness | BPs per turn | Diameter () | Pitch () | BP inclination | Sugar pucker |
|---|---|---|---|---|---|---|
| B-DNA | Right | 10 | 20 | 34 | 0° | C2’-endo |
| A-DNA/A-RNA | Right | 11 | 26 | 28 | 20° | C3’-endo |
| Z-DNA | Left | 12 | 18 | 45 | -7° | alternating[12] |
3.2Other tertiary motifs¶
Other important tertiary motifs are those that can connect more than two strands together, or two sections of the same strand that are far apart from each other. For instances, in triplexes (i.e. triple-stranded DNA or RNA) a third strand can bind in the major groove of a duplex through Hoogsteen base pairings, or in RNA in the minor groove by leveraging the presence of the additional hydroxyl group in the sugar.
Figure 11:Example of a G-quadruplex, showing (left) one layer and (right) the full stacked structure. Credits to Julian Huppert and Iridos via Wikipedia Commons.
Hoogsteen base pairings can also lead to the formation of quadruplexes, which can occur in a variety of patterns, including intramolecular (within a single strand), intermolecular (between different strands), and hybrid types. A strand (or multiple strands) with a high number of consecutive guanine bases folds back on itself (or aligns with other strands) to bring the G bases into proximity. As sketched in Figure 11 Four guanine bases form a planar structure known as a G-tetrad through Hoogsteen hydrogen bonding, and multiple G-tetrads stack on top of each other, stabilized by the interactions between the aromatic rings of the guanine bases.
Finally, as mentioned earlier, pseudoknots and coaxial stacking interactions can also seen as mechanisms the can lead to the formation of particular tertiary structures, since they can stabilise multi-strand (or multi-loop) structures.
Here I simplify, since chemical modifications are possible (e.g. methylation), and sometimes U and T can end up in DNA and RNA, respectively.
and also U, A and C can bind to the non-standard nucleotide hypoxanthine.
Of course, this argument applies to solutions of nucleic acids only. In the cell, RNA, DNA, and proteins can and do interact together to form higher order structures.
“You mean [that a double helix can form] without an enzyme?” Rich (2009)
This is already an approximation, since some non-canonical (e.g. Hoogsteen) base pairings can connect a nucleotide to another which is already involved in a base pair.
There is one aminoacyl-tRNA synthetase for each amino acid of the genetic code: in humans, there are 20.
m: 2-methyl-guanosine, D: 5,6-Dihydrouridine, mG: N2-dimethylguanosine, C: O2’-methyl-cytdine, G: O2’-methyl-guanosine, T: 5-Methyluridine (Ribothymidine), Y: wybutosine (Y-base), : pseudouridine, m: 5-methyl-cytidine, m: 7-methyl-guanosine, m: 1-methyl-adenosine.
Magnesium and other multivalent cations are not supported.
The two-state model can be applied to all those cases where two objects can reversibly bind and unbind (e.g. two proteins, or a protein and a small molecule)
If we can neglect the interaction between different strands, i.e. if the overall concentration is low enough that we can assume ideal gas behaviour.
In both cases the A form is thought to protect the genetic material from extreme conditions.
The alternating pyrimidines and purines take the C2’-endo and C3’-endo conformations, respectively.
- Lehninger, A. L., Nelson, D. L., & Cox, M. M. (2005). Lehninger principles of biochemistry. Macmillan.
- Schlick, T. (2010). Molecular modeling and simulation: an interdisciplinary guide (Vol. 2). Springer.
- WATSON, J. D., & CRICK, F. H. C. (1953). Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid. Nature, 171(4356), 737–738. 10.1038/171737a0
- Voet, D., & Rich, A. (1970). The Crystal Structures of Purines, Pyrimidines and Their Intermolecular Complexes. In Progress in Nucleic Acid Research and Molecular Biology (pp. 183–265). Elsevier. 10.1016/s0079-6603(08)60565-6
- Rich, A. (2009). The Era of RNA Awakening: Structural biology of RNA in the early years. Quarterly Reviews of Biophysics, 42(2), 117–137. 10.1017/s0033583509004776
- Yakovchuk, P. (2006). Base-stacking and base-pairing contributions into thermal stability of the DNA double helix. Nucleic Acids Research, 34(2), 564–574. 10.1093/nar/gkj454
- Vologodskii, A., & Frank-Kamenetskii, M. D. (2018). DNA melting and energetics of the double helix. Physics of Life Reviews, 25, 1–21. 10.1016/j.plrev.2017.11.012
- Banerjee, A., Anand, M., Kalita, S., & Ganji, M. (2023). Single-molecule analysis of DNA base-stacking energetics using patterned DNA nanostructures. Nature Nanotechnology, 18(12), 1474–1482. 10.1038/s41565-023-01485-1
- Protozanova, E., Yakovchuk, P., & Frank-Kamenetskii, M. D. (2004). Stacked–Unstacked Equilibrium at the Nick Site of DNA. Journal of Molecular Biology, 342(3), 775–785. 10.1016/j.jmb.2004.07.075
- SantaLucia, J., Jr., & Hicks, D. (2004). The Thermodynamics of DNA Structural Motifs. Annual Review of Biophysics and Biomolecular Structure, 33(1), 415–440. 10.1146/annurev.biophys.32.110601.141800
- Lu, Z. J., Turner, D. H., & Mathews, D. H. (2006). A set of nearest neighbor parameters for predicting the enthalpy change of RNA secondary structure formation. Nucleic Acids Research, 34(17), 4912–4924. 10.1093/nar/gkl472
- Zuber, J., Schroeder, S. J., Sun, H., Turner, D. H., & Mathews, D. H. (2022). Nearest neighbor rules for RNA helix folding thermodynamics: improved end effects. Nucleic Acids Research, 50(9), 5251–5262. 10.1093/nar/gkac261
- Snodin, B. E. K., Randisi, F., Mosayebi, M., Šulc, P., Schreck, J. S., Romano, F., Ouldridge, T. E., Tsukanov, R., Nir, E., Louis, A. A., & Doye, J. P. K. (2015). Introducing improved structural properties and salt dependence into a coarse-grained model of DNA. The Journal of Chemical Physics, 142(23). 10.1063/1.4921957
- Sharma, R., Patelli, A. S., De Bruin, L., & Maddocks, J. H. (2023). cgNA+web : A Visual Interface to the cgNA+ Sequence-dependent Statistical Mechanics Model of Double-stranded Nucleic Acids. Journal of Molecular Biology, 435(14), 167978. 10.1016/j.jmb.2023.167978