Observables¶

`BondOrderParameters`
`ClusterList`	Partition particles into clusters.
`CollectiveISF`	Compute the spatial Fourier transform of the van Hove function, also known as the intermediate scattering function (ISF) \(F_c(q, t)\), of a trajectory.
`ConvexHull`	Construct the convex hull of the system, which is the smallest convex set that contains the particles’ coordinates.
`FormFactor`	Compute the form factor of a system or the average form factor of the molecules contained in the system.
`GyrationRadius`	Compute the gyration radius of a system or the average gyration radius of the molecules contained in the system.
`MSD`	Compute the mean-squared displacement of a trajectory.
`ParticleAutocorrelation`	Compute the normalised autocorrelation of particle-related three-dimensional vectors.
`PoreSize`	Find the pore sizes of a system.
`RDF`	Compute the radial distribution function (RDF) of a system.
`SelfISF`	Compute the self part of the spatial Fourier transform of the van Hove function, also known as the intermediate scattering function (ISF) \(F_s(q, t)\), of a trajectory.
`StructureFactor`	Compute the structure factor of a system.

class baggianalysis.core.BondOrderParameters(self: baggianalysis.core.BondOrderParameters, orders_to_compute: Set[int], compute_avg_qs: bool = True, compute_qs: bool = False, compute_avg_ws: bool = False, compute_ws: bool = False) → None ¶

Bases: pybind11_builtins.pybind11_object

analyse_system(self: baggianalysis.core.BondOrderParameters, arg0: baggianalysis.core.System) → None ¶

analyse_trajectory(self: baggianalysis.core.BondOrderParameters, arg0: baggianalysis.core.BaseTrajectory) → None ¶

reset(self: baggianalysis.core.BondOrderParameters) → None ¶

result(self: baggianalysis.core.BondOrderParameters) → List[List[float]]¶

class baggianalysis.core.ClusterList(self: baggianalysis.core.ClusterList) → None ¶

Bases: pybind11_builtins.pybind11_object

Partition particles into clusters. The result of the computation is a list of the sizes of all clusters.

The default constructor takes no parameters

analyse_system(self: baggianalysis.core.ClusterList, arg0: baggianalysis.core.System) → None ¶

analyse_trajectory(self: baggianalysis.core.ClusterList, arg0: baggianalysis.core.BaseTrajectory) → None ¶

property clusters¶: Return the list of clusters of the system analysed last.

reset(self: baggianalysis.core.ClusterList) → None ¶

result(self: baggianalysis.core.ClusterList) → List[int]¶

class baggianalysis.core.CollectiveISF(*args, **kwargs)¶

Bases: pybind11_builtins.pybind11_object

Compute the spatial Fourier transform of the van Hove function, also known as the intermediate scattering function (ISF) \(F_c(q, t)\), of a trajectory.

The trajectory is split up in chunks of size points_per_cycle, and the collective ISF is computed between configurations in each chunk and between the initial configurations of pairs of chunks for different wave vectors \(q\).

The collective ISF between two configurations is associated to their time delta (i.e. to the difference between the times at which they have been printed) and averaged with all the other pairs that share the same time delta. Note that in same cases (i.e. log or log-linear spacing), there might be time deltas that differ by one: in this case the code consider those pairs to share the same time delta.

Overloaded function.

__init__(self: baggianalysis.core.CollectiveISF, largest_q: float, max_n_realisations: int, max_delta_q: float, points_per_cycle: int) -> None

Parameters

largest_q (float) – The length of the largest q vector of interest
max_n_realisations (int) – Given a length \(q\), this is the maximum number of q vectors that will be averaged over to compute \(F_s(q, t)\)
max_delta_q (float) – q-vectors that are separated by distances smaller than this value will be assigned to the same value of \(q\)
points_per_cycle (int) – The number of configurations contained in each chunk in which the trajectory is split up.

__init__(self: baggianalysis.core.CollectiveISF, q_vectors: ba::WaveVectorList, points_per_cycle: int) -> None

Parameters

q_vectors (WaveVectorList) – The list of q vectors that will be used to compute the collective ISF.
points_per_cycle (int) – The number of configurations contained in each chunk in which the trajectory is split up.

analyse_and_print(self: baggianalysis.core.CollectiveISF, trajectory: baggianalysis.core.BaseTrajectory, output_file: str, normalise: bool = True) → None ¶

Analyse the trajectory and print the collective ISF directly to the given file.

Parameters

trajectory (BaseTrajectory) – The trajectory to be analysed
output_file (string) – The output filename
normalise (bool) – Normalise the correlation functions so that they start from 1 at time zero. Defaults to true.

analyse_trajectory(self: baggianalysis.core.CollectiveISF, arg0: baggianalysis.core.BaseTrajectory) → None ¶

reset(self: baggianalysis.core.CollectiveISF) → None ¶

result(self: baggianalysis.core.CollectiveISF) → Dict[int, List[float]]¶

class baggianalysis.core.ConvexHull(self: baggianalysis.core.ConvexHull) → None ¶

Bases: pybind11_builtins.pybind11_object

Construct the convex hull of the system, which is the smallest convex set that contains the particles’ coordinates.

analyse_system(self: baggianalysis.core.ConvexHull, arg0: baggianalysis.core.System) → None ¶

analyse_trajectory(self: baggianalysis.core.ConvexHull, arg0: baggianalysis.core.BaseTrajectory) → None ¶

reset(self: baggianalysis.core.ConvexHull) → None ¶

result(self: baggianalysis.core.ConvexHull) → ba::ConvexHullResult¶

class baggianalysis.core.ConvexHullResult(self: baggianalysis.core.ConvexHullResult) → None ¶

Bases: pybind11_builtins.pybind11_object

The actual convex hull.

property area¶: The area of the convex hull.

property triangles¶: A list of Triangles that compose the convex hull.

property vertices¶: The vertices that compose the convex hull. These are a subset of the particles of the system.

property volume¶: The volume of the convex hull.

class baggianalysis.core.ConvexHullTriangle¶

Bases: pybind11_builtins.pybind11_object

A triangle of the convex hull mesh. It contains its three vertices as well as its normal (i.e. the normal unit vector pointing outwards).

area(self: baggianalysis.core.ConvexHullTriangle) → float ¶: Return the area of the triangle.

property normal¶: The unit vector orthogonal to the triangle surface which points towards the exterior of convex hull.

property v1¶: The first vertex.

property v2¶: The second vertex along the counter-clock-wise contour of the triangle.

property v3¶: The second vertex along the counter-clock-wise contour of the triangle.

volume(self: baggianalysis.core.ConvexHullTriangle) → float ¶: Return the volume of the triangle.

class baggianalysis.core.FormFactor(self: baggianalysis.core.FormFactor, q_modules: List[float], q_repetitions: int, compute_on_molecules: bool) → None ¶

Bases: pybind11_builtins.pybind11_object

Compute the form factor of a system or the average form factor of the molecules contained in the system.

The mathematical definition of the form factor is the same as structure factor, with the difference that the form factor is to be intended as the scattering response of single objects. As a result, the size of the simulation box does not set the smallest wave vector that can be used in its computation.

Parameters

q_modules (List(float)) – The modules of the wave vectors that will be used to compute the form factor.
q_repetitions (int) – The number of random realisations of each wave vector module that will be used to compute the form factor.
compute_on_molecules (bool) – If True, the final form factor will be computed as the average form factor of the molecules composing the system.

analyse_particle_set(self: baggianalysis.core.FormFactor, p_set: baggianalysis.core.ParticleSet) → None ¶

Compute the form factor of the given ParticleSet.

Parameters: p_set (ParticleSet) – The object containing the input particles.

analyse_system(self: baggianalysis.core.FormFactor, arg0: baggianalysis.core.System) → None ¶

analyse_trajectory(self: baggianalysis.core.FormFactor, arg0: baggianalysis.core.BaseTrajectory) → None ¶

clear_b_factors(self: baggianalysis.core.FormFactor) → None ¶: Reset the b-factors to their default values (b = 1 for each particle).

reset(self: baggianalysis.core.FormFactor) → None ¶

result(self: baggianalysis.core.FormFactor) → Dict[float, float]¶

set_b_factors(self: baggianalysis.core.FormFactor, b_factors: List[float]) → None ¶

Set the particles’ b-factors (that is, the scattering amplitudes) that will be used to compute the form factor.

Parameters: b_factors (List(float)) – The vector of b-factors to be used in the calculation of the P(q). The length of the vector should be equal to the number of particles in the system.

class baggianalysis.core.GyrationRadius(self: baggianalysis.core.GyrationRadius, compute_on_molecules: bool) → None ¶

Bases: pybind11_builtins.pybind11_object

Compute the gyration radius of a system or the average gyration radius of the molecules contained in the system.

Parameters: compute_on_molecules (bool) – If True, the final gyration radius will be computed as the average gyration radius of the molecules composing the system.

analyse_particle_set(self: baggianalysis.core.GyrationRadius, p_set: baggianalysis.core.ParticleSet, box: glm::tvec3<scalar, P>) → None ¶

Compute the gyration radius of the given ParticleSet.

Parameters

p_set (ParticleSet) – The object containing the input particles.
box (numpy.ndarray) – The simulation box.

analyse_system(self: baggianalysis.core.GyrationRadius, arg0: baggianalysis.core.System) → None ¶

analyse_trajectory(self: baggianalysis.core.GyrationRadius, arg0: baggianalysis.core.BaseTrajectory) → None ¶

reset(self: baggianalysis.core.GyrationRadius) → None ¶

result(self: baggianalysis.core.GyrationRadius) → float ¶

class baggianalysis.core.MSD(self: baggianalysis.core.MSD, points_per_cycle: int, remove_com: bool = True) → None ¶

Bases: pybind11_builtins.pybind11_object

Compute the mean-squared displacement of a trajectory.

The trajectory is split up in chunks of size points_per_cycle, and the mean squared displacement is computed between configurations in each chunk and between the initial configurations of pairs of chunks.

The mean squared displacement between two configurations is associated to their time delta (i.e. to the difference between the times at which they have been printed) and averaged with all the other pairs that share the same time delta. Note that in same cases (i.e. log or log-linear spacing), there might be time deltas that differ by one: in this case the code consider those pairs to share the same time delta.

Parameters

points_per_cycle (int) – The number of configurations contained in each chunk in which the trajectory is split up.
remove_com (bool) – Remove the centre of mass’ position from each configuration.

analyse_and_print(self: baggianalysis.core.MSD, trajectory: baggianalysis.core.BaseTrajectory, output_file: str) → None ¶: Analyse the trajectory and print the MSD directly to the given file.

analyse_trajectory(self: baggianalysis.core.MSD, arg0: baggianalysis.core.BaseTrajectory) → None ¶

reset(self: baggianalysis.core.MSD) → None ¶

result(self: baggianalysis.core.MSD) → Dict[int, float]¶

class baggianalysis.core.ParticleAutocorrelation(self: baggianalysis.core.ParticleAutocorrelation, points_per_cycle: int, function: Callable[[baggianalysis.core.Particle], glm::tvec3<scalar, P>], normalise: bool = False) → None ¶

Bases: pybind11_builtins.pybind11_object

Compute the normalised autocorrelation of particle-related three-dimensional vectors.

The constructor takes a function that will be used on each particle to return the three-dimensional vector whose autocorrelation will be computed. As an example, the two observables defined below will compute the velocity and angular velocity autocorrelation functions:

v_obs = ba.ParticleAutocorrelation(30, lambda p: p.velocity)
omega_obs = ba.ParticleAutocorrelation(30, lambda p: p.angular_velocity)

The trajectory is split up in chunks of size points_per_cycle, and the autocorrelation is computed between configurations in each chunk and between the initial configurations of pairs of chunks.

Parameters

points_per_cycle (int) – The number of configurations contained in each chunk in which the trajectory is split up.
function (callable) – A callable that takes a particle and returns the three-dimensional vector whose autocorrelation will be computed.
normalise (bool) – If True, the the autocorrelation will be normalised (i.e. its value in 0 will be 1). Defaults to False.

analyse_and_print(self: baggianalysis.core.ParticleAutocorrelation, trajectory: baggianalysis.core.BaseTrajectory, output_file: str) → None ¶: Analyse the trajectory and print the autocorrelation directly to the given file.

analyse_trajectory(self: baggianalysis.core.ParticleAutocorrelation, arg0: baggianalysis.core.BaseTrajectory) → None ¶

reset(self: baggianalysis.core.ParticleAutocorrelation) → None ¶

result(self: baggianalysis.core.ParticleAutocorrelation) → Dict[int, float]¶

class baggianalysis.core.PoreSize(self: baggianalysis.core.PoreSize, N_attempts: int, r_cut: float = 1.0, particle_radius: float = 0.5, max_time: float = 1.0) → None ¶

Bases: pybind11_builtins.pybind11_object

Find the pore sizes of a system. Requires NLopt.

The pore size distribution \(P_G(r)\) is defined as in Bhattacharya and Gubbins (2006). The algorithm is schematically represented in the following figure (taken from Sorichetti, Hugovieux and Kob (2020), where the algorithm was applied to a polymeric system):

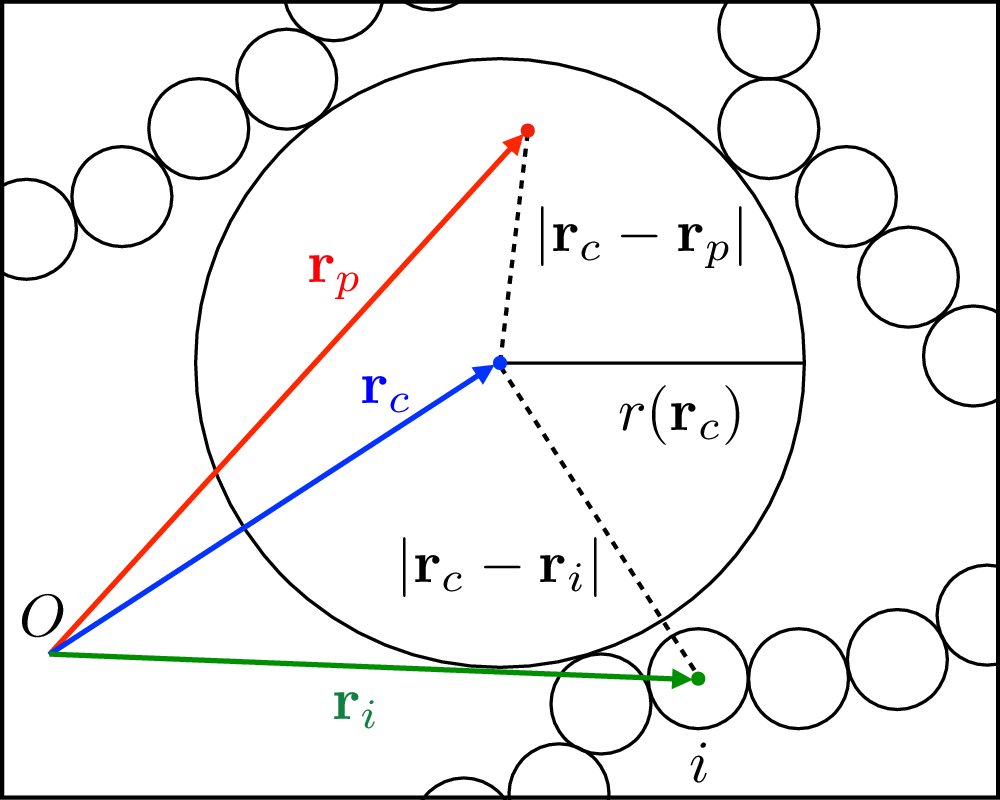
Given a randomly chosen point \(\mathbf r_p\) in the void phase, one has to find the sphere with the largest radius \(r\) containing \(\mathbf r_p\) and which does not overlap with any particle. This problem can be reformulated as that of maximizing the function

\[r(\mathbf r_c) \equiv \min_{i=1,\dots M} \{|\mathbf r_c - \mathbf r_i|\} - \sigma/2, \label{obj_function}\]

subject to the constraint

\[|\mathbf r_c-\mathbf r_p| - r(\mathbf r_c) \leq 0,\]

where \(\mathbf r_c\) is the position of the sphere’s center and \(\mathbf r_i\) are the positions of the centers of the particles. If the maximization of the function above is carried out for a large enough number of points \(\mathbf r_p\), the resulting (normalized) histogram of \(r\) values will converge to \(P_G(r)\).

The problem of calculating \(P_G(r)\) reduces therefore to a nonlinear optimization problem, which can be solved with a standard algorithm. Here we use the open-source Sbplx algorithm of the NLopt library, which can handle discontinuous objective functions.

The constructur builds an observable that computes N_attempts different pore sizes by applying the algorithm described above for N_attempts random values of \(r_p\).

Parameters

N_attempts (int) – The number of pore size evaluations that will be carried out per system.
r_cut (float) – The characteristic size of the particle-particle repulsion. Using the right number will speed up the computation but does not impact the quality of the results.
particle_radius (float) – The radius of the particles stored in the system. This is usually half r_cut.
max_time (float) – The timeout (in seconds) beyond which NLopt will stop looking for a solution to the optimisation problem.

analyse_system(self: baggianalysis.core.PoreSize, arg0: baggianalysis.core.System) → None ¶

analyse_trajectory(self: baggianalysis.core.PoreSize, arg0: baggianalysis.core.BaseTrajectory) → None ¶

radius(self: baggianalysis.core.PoreSize, centre: glm::tvec3<scalar, P>) → float ¶

Calculates the radius of the largest sphere centred in centre that does not overlap with any of the particles.

Parameters: centre (numpy.ndarray) – The reference position
Returns: The radius of the largest sphere centred in centre that does not overlap with any of the particles.
Return type: float

reset(self: baggianalysis.core.PoreSize) → None ¶

result(self: baggianalysis.core.PoreSize) → List[float]¶

class baggianalysis.core.RDF(*args, **kwargs)¶

Bases: pybind11_builtins.pybind11_object

Compute the radial distribution function (RDF) of a system.

Overloaded function.

__init__(self: baggianalysis.core.RDF, arg0: float) -> None

Parameters: bin_size (float) – The width of the histogram bins

__init__(self: baggianalysis.core.RDF, arg0: float, arg1: float) -> None

Parameters

bin_size (float) – The width of the histogram bins
max_value (float) – The largest distance that will be considered

__init__(self: baggianalysis.core.RDF, arg0: float, arg1: List[str], arg2: List[str]) -> None

This constructor makes it possible to select those pairs of particles that will contribute to the RDF, based on their types.

The constuctor takes two additional parameters that specify the lists of types that should be included. A pair of particles p and q will be considered in the RDF only if the type of p is in the first list and the type of q is in the second list, or vice versa. For instance, the following snippet will create an RDF observable that will take into account only A-A and A-B pairs:

RDF = ba.RDF(0.1, ["A"], ["A", "B"]) # equivalent to RDF = ba.RDF(0.1, ["A", "B"], ["A"])

Parameters

bin_size (float) – The width of the histogram bins
types_1 (List(str)) – The first group of particle types
types_2 (List(str)) – The second group of particle types

__init__(self: baggianalysis.core.RDF, arg0: float, arg1: float, arg2: List[str], arg3: List[str]) -> None

Similar to the constructor above, with the difference that the largest distance that will be used in the computation can also be specified.

Parameters

bin_size (float) – The width of the histogram bins
max_value (float) – The largest distance that will be considered
types_1 (List(str)) – The first group of particle types
types_2 (List(str)) – The second group of particle types

analyse_system(self: baggianalysis.core.RDF, arg0: baggianalysis.core.System) → None ¶

analyse_trajectory(self: baggianalysis.core.RDF, arg0: baggianalysis.core.BaseTrajectory) → None ¶

reset(self: baggianalysis.core.RDF) → None ¶

result(self: baggianalysis.core.RDF) → Dict[float, float]¶

class baggianalysis.core.SelfISF(*args, **kwargs)¶

Bases: pybind11_builtins.pybind11_object

Compute the self part of the spatial Fourier transform of the van Hove function, also known as the intermediate scattering function (ISF) \(F_s(q, t)\), of a trajectory.

The trajectory is split up in chunks of size points_per_cycle, and the self ISF is computed between configurations in each chunk and between the initial configurations of pairs of chunks for different wave vectors \(q\).

The self ISF between two configurations is associated to their time delta (i.e. to the difference between the times at which they have been printed) and averaged with all the other pairs that share the same time delta. Note that in same cases (i.e. log or log-linear spacing), there might be time deltas that differ by one: in this case the code consider those pairs to share the same time delta.

Overloaded function.

__init__(self: baggianalysis.core.SelfISF, largest_q: float, max_n_realisations: int, max_delta_q: float, points_per_cycle: int) -> None

Parameters

largest_q (float) – The length of the largest q vector of interest
max_n_realisations (int) – Given a length \(q\), this is the maximum number of q vectors that will be averaged over to compute \(F_s(q, t)\)
max_delta_q (float) – q-vectors that are separated by distances smaller than this value will be assigned to the same value of \(q\)
points_per_cycle (int) – The number of configurations contained in each chunk in which the trajectory is split up.

__init__(self: baggianalysis.core.SelfISF, q_vectors: ba::WaveVectorList, max_n_realisations: int) -> None

Parameters

q_vectors (WaveVectorList) – The list of q vectors that will be used to compute the self ISF.
points_per_cycle (int) – The number of configurations contained in each chunk in which the trajectory is split up.

analyse_and_print(self: baggianalysis.core.SelfISF, trajectory: baggianalysis.core.BaseTrajectory, output_file: str) → None ¶: Analyse the trajectory and print the self ISF directly to the given file.

analyse_trajectory(self: baggianalysis.core.SelfISF, arg0: baggianalysis.core.BaseTrajectory) → None ¶

reset(self: baggianalysis.core.SelfISF) → None ¶

result(self: baggianalysis.core.SelfISF) → Dict[int, List[float]]¶

class baggianalysis.core.StructureFactor(*args, **kwargs)¶

Bases: pybind11_builtins.pybind11_object

Compute the structure factor of a system.

Overloaded function.

__init__(self: baggianalysis.core.StructureFactor, largest_q: float, max_n_realisations: int, max_delta_q: float) -> None

Parameters

largest_q (float) – The length of the largest q vector of interest
max_n_realisations (int) – Given a length \(q\), this is the maximum number of q vectors that will be averaged over to compute \(F_s(q, t)\)
max_delta_q (float) – q-vectors that are separated by distances smaller than this value will be assigned to the same value of \(q\)

__init__(self: baggianalysis.core.StructureFactor, q_vectors: ba::WaveVectorList) -> None

Parameters

q_vectors (WaveVectorList) – The list of q vectors that will be used to compute the self ISF.
points_per_cycle (int) – The number of configurations contained in each chunk in which the trajectory is split up.

analyse_system(self: baggianalysis.core.StructureFactor, arg0: baggianalysis.core.System) → None ¶

analyse_trajectory(self: baggianalysis.core.StructureFactor, arg0: baggianalysis.core.BaseTrajectory) → None ¶

clear_b_factors(self: baggianalysis.core.StructureFactor) → None ¶: Reset the b-factors to their default values (b = 1 for each particle).

destructured_from_system(self: baggianalysis.core.StructureFactor, system: baggianalysis.core.System) → baggianalysis.core.DestructuredStructureFactor ¶

Compute and return the single-particle contributions (splitted as cosine and sine contributions stored in a DestructuredStructureFactor instance) that make up the structure factor.

Parameters: system (System) – The input system.
Returns: The final result of the computation.
Return type: DestructuredStructureFactor

reset(self: baggianalysis.core.StructureFactor) → None ¶

result(self: baggianalysis.core.StructureFactor) → Dict[float, float]¶

set_b_factors(self: baggianalysis.core.StructureFactor, b_factors: List[float]) → None ¶

Set the particles’ b-factors (that is, the scattering amplitudes) that will be used to compute the structure factor.

Parameters: b_factors (List(float)) – The vector of b-factors to be used in the calculation of the S(q). The length of the vector should be equal to the number of particles in the system.

class baggianalysis.core.DestructuredStructureFactor(self: baggianalysis.core.DestructuredStructureFactor) → None ¶

Bases: pybind11_builtins.pybind11_object

property cos_contribs¶

property q_modules¶

property sin_contribs¶